【技术专区】LED 封装器件芯片结温测试浅述（下）

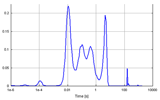
　　大家应该还记得在《LED 封装器件芯片结温测试浅述(上)》里面我们有提及到 “电流跳变”的瞬态测试方法，如果我们在跳变之后不断地采集电压信号，直到器件冷却到环境温度，我们就可以得到LED在降温过程中它的电压随时间的变化曲线，又因为这些电压变化都是在测试电流下得到的，我们只需要把电压信号除以K系数就可以得到温度变化随时间的曲线(因为k=Δv/Δt)，温度变化曲线如图1所示：

图1 温度变化-时间曲线

　　时间对数化

　　事实上，图1中的时间轴是经过对数化处理的，因为实际进行采样时我们是得益于设备的高速采样可以在1μs(即10^-6s)后采集到第一个电压的变化值，但采样总时间的数量级一般都在1s～10³s范围内，时间的数量级跨度大而且时间越往后温度变化就越慢，数据的重要度也随之降低，因此在数据处理时我们把时间进行对数化处理。时间对数化后的曲线如图2b所示。

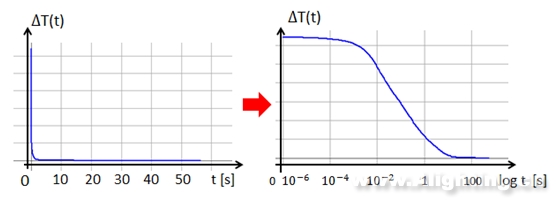
图2a温度变化响应曲线 图2b温度变化响应曲线(时间对数化后)

　　对比图2a和图2b可以发现，对数前处理前的数据变化不直观，对数化处理后却能把瞬态切换后几微秒内的温度变化充分表示出来。后文在计算中也要用到时间对数化的推导。

　　这次我们就用这个曲线来获得我们神奇的结构函数。首先要介绍一下：

　　阻容网络的物理模型

　　首先，我们需要构造一个导热的模型。不如先从简单开始，假设热源到环境的导热只有一个路径，而且是一种材料，这种材料是各向同性而且形状规则，有一定的热阻与热容，习惯上我们也同样用电阻电容的符号来代表热阻和热容，热源从材料的左表面流到右表面(环境)，如图3所示。

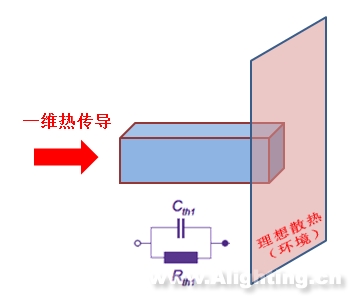
图3热传导模型图示及RC网络

　　在这个简单的模型里，我们看到这样的一个RC(阻容)网络，如图4，在这个网络里，热源当作一个恒流源，而热阻与热容并联到环境，我们称之为一阶RC网络。

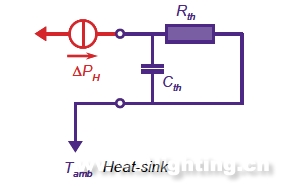
图4 一阶RC网络

　　在数字信号处理领域，通常都是利用一个系统的响应再把系统的结构分析出来。所谓响应就是系统在某一特定信号源的激励下产生的反应(输出特性)，比如有人在你身后喊了一声你的名字，有的人会回头望而有的人不回头只是应了一声。不同的系统会有不同的响应，同一个系统在不同信号的激励下也会有不同的响应。

　　现在我们把这个一阶RC网络看成一个系统，那要用什么信号做激励呢?其实文初我们提到的“电流跳变”就可以做为一个信号源，一般我们把这种电流跳变信号称为单位阶跃信号，因为它的信号就像台阶一样突然从低跳到高(或从高到低)，那这个系统在单位阶跃信号激励下的响应是怎样的呢?

　　如果输入信号是单位阶跃信号，则这个系统的响应我们简称为该系统的单位阶跃响应。

　　那么一阶RC网络的单位阶跃响应为

图5 一阶RC网络及对应的时间常数图

　　式1中的 τ我们称为时间常数，它是信号处理领域里的常用的表征时间的物理量，其量纲单位和时间一样，也是秒[s]。时间常数的含义是指某物理量从最大值衰减到最大值的1/e(或从最小值增加到最大值的1-1/e倍)所需要的时间，比如一个满电荷的电容两端并联一个电阻，那么电容两端的电压从最大值放电到最大值的1/e倍所花的时间就是 。

　　这里我们称τ为“热时间常数”以示区分，因为它代表的是热阻与热容的乘积。

　　现在我们把结构的数量从1个升级到n个，那么就会变成n阶RC网络，如图6所示。

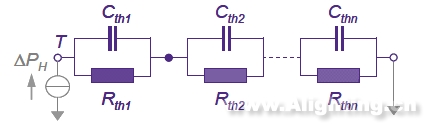
图6 n阶RC网络

　　其对应的单位阶跃响应为

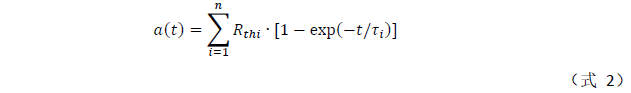
　　一般我们把这种结构的RC网络称为n阶福斯特(Foster)结构，其对应的热时间常数谱如图7所示。

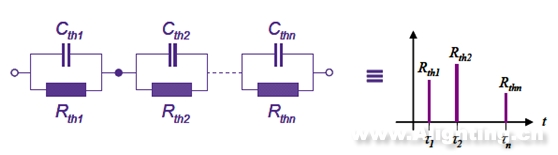
图7 n阶福斯特结构的热时间常数图

　　实际上，材料与材料之间的交接界面是同样存在热阻与热容的，器件各材料之间也不可能完全看成独立成单一的热阻热容，我们应该认为热阻与热容的变化是连续的，于是我们需要把这个离散的多项式进行连续化处理，也就是当n趋向于正无穷的时候，可把(式2)改为

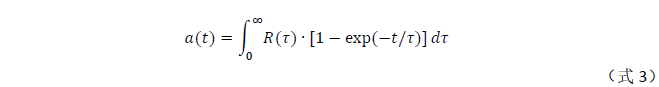
　　(式3)中的R（τ）称为时间常数谱函数，我们用连续的R（τ）来取代离散的R_thi 。它的时间常数图为连续谱图，如图8所示。

图8 连续谱图

　　(式3)这个公式代表的就是一个连续RC网络的单位阶跃响应。

　　看回文初的图1b温度变化曲线，事实上这个曲线在对数化处理前对应的表达式就是

　　求解热时间常数谱函数

　　我们再看回R（τ），其实如果我们知道了R（τ）的表达式，那么我们就相当于知道了这个系统的热阻和热容的关系，也就是知道了这个系统(福斯特网络)的所有结构。那么为了得到我们系统的热阻热容结构，下面就开始把R（τ）求出来：

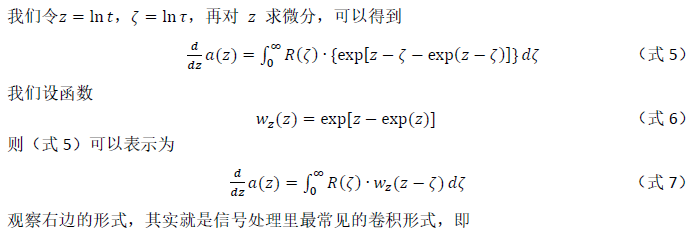
　　观察右边的形式，其实就是信号处理里最常见的卷积形式，即

　　到这里我们就得到了R（τ）的解析式，离结构还差一步之遥!

　　我们看看(式9)，W_z（Z）是已知的可积函数，d／dz·a（z）是单位阶跃响应(时间对数化后)的微分，也就是导数，我们都可以用计算机算出来。剩下的就只有反卷积运算了。反卷积运算的方法有很多，比如有贝叶斯反卷积法以及傅利叶频域反卷积法，都是很成熟的算法，这里要涉及的知识较多，就不一一展开了。

　　现在我们得到了R（z）——热时间常数谱函数，它实际的图像如图9所示。

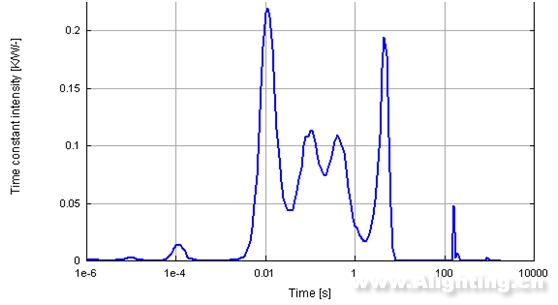
图9 实际样品的热时间常数谱图

　　这个函数图像就是经过上述的数学变换及数学运算得出来的，我们下面就利用这个函数把热阻热容结构剖析出来。

　　从图里我们可以明显看出对应不同的 其幅值有不同起伏变化，表现出一定的离散性，我们就由此来定义这个热时间常数谱函数：

　　简单来说就是把这个函数切成无数个小块，把这些小块都拼接起来就是R（ζ）了。而这每一个小块就是对应1阶福斯特结构，如图10所示。

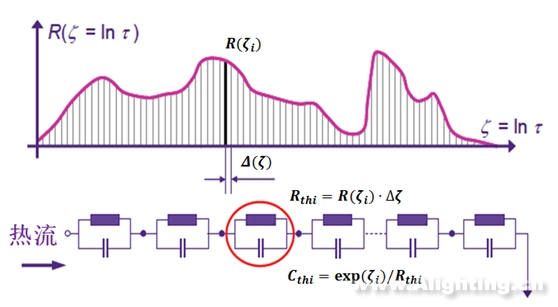
图10 热时间常数谱函数图像与n阶福斯特网络对应关系

　　根据 的定义，我们可以得到

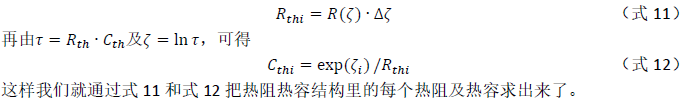
　　福斯特-考尔网络转换

　　很多读者应该会认为到这里已经结束了，但事实上，这只是对应福斯特网络的热阻热容值，

　　而在福斯特网络这个模型里的热容是节点到节点的热容值，它与器件的实际情况不一致，是没有对应的物理意义的。为什么呢?这里我们把这个小问题留给大家(提示：用电容来举例，假如一个系统由若干个电容串联，系统的总容值与各个电容的关系怎么算?)。因此福斯特结构并不适合描述我们半导体器件的热阻热容特性。

　　虽然福斯特结构不适合用来描述我们实际器件的情形，但有另一种结构却可以与它相互转换，这个结构我们称为考尔(Cauer)结构，如图11所示。

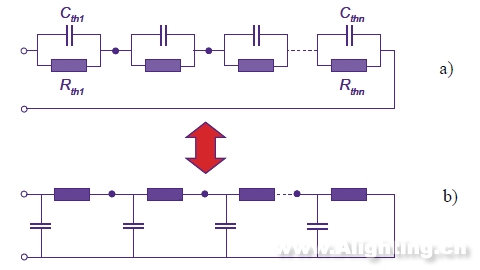
图11 a)福斯特结构;b)考尔结构

　　福斯特结构与考尔结构对于单端无源RC网络都是等价的，因为他们可以相互转换，但考尔结构与我们谈到的器件的热阻热容结构可以说是完全吻合，我们之所以谈了这么多福斯特结构是因为它的时间常数计算是一种很优秀的数学手段，同时减少了很多复杂的计算。

　　由于篇幅有限，这两个网络的转换过程我们这里就不做多述了，经过转换之后我们会得到的R_thi和C_thi的新的表达形式。

　　绘制结构函数

　　我们得到了考尔网络对应下的热阻R_thi和热容C_thi，但这些参数都不能直观地表示出来，我们现在用图3构造的模型把这个阻容结构表示出来，如图12所示。

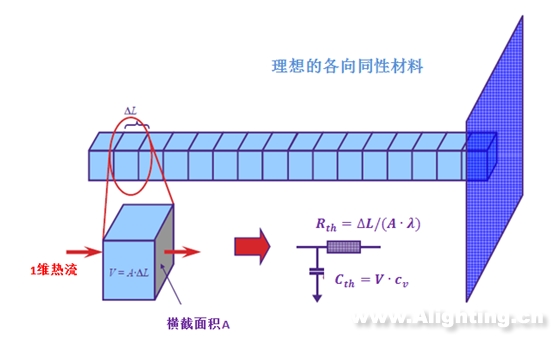
图12 理想一维热传导模型

　　图12中： 表示平行于热流路径的材料厚度;A表示垂直于热流路径的材料横截面积; 表示材料的热导率; 表示单位体积的热容值。我们可以得出总热阻与总热容的表达式：

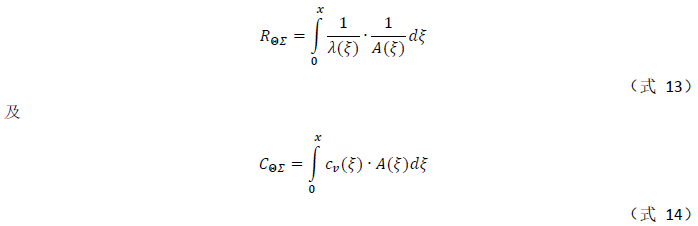
　　利用(式13)与(式14)，与考尔网络对应下的热阻R_thi和热容C_thi结合，我们就得到我们苦苦追求的结构函数，如图13所示：

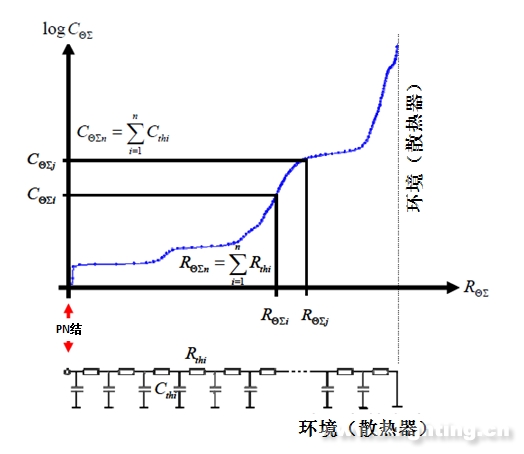
图13 考尔结构与结构函数的对应

　　至此我们对结构函数的推导终于结束了～

　　在最后，我们再把整个推导用流程图的方式展示出来，如图14所示：

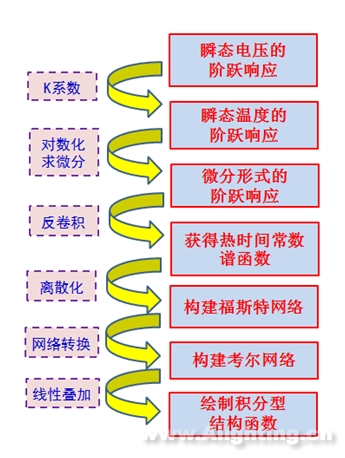
图14 结构函数推导流程图